Introduction: Understanding the Foundation of Digital Circuits
Have you ever wondered how your computer makes decisions? Behind every digital device we use daily from smartphones to laptops to smart
home devices lies a complex network of circuits built on simple logical operations. At the heart of these operations is a concept known as the sum of
products. The sum of products is a fundamental concept in digital logic design that represents Boolean functions as a logical OR of AND terms.
It’s one of those ideas that might seem abstract at first, but once you grasp it, you’ll see how it shapes the digital world around us.
In this guide, I’ll walk you through everything you need to know about sum of products expressions from basic definitions to practical applications. Whether you’re a student struggling with digital electronics homework, an engineer looking to refresh your knowledge, or just someone curious about how computers “think,” this article has something for you.
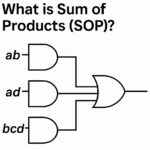
What is Sum of Products (SOP)?
Sum of products (SOP) is a way to express Boolean functions in digital logic. Despite its mathematical-sounding name, the concept is actually quite straightforward. In Boolean algebra, a sum of products expression consists of multiple AND terms (products) combined using OR operations (sums). Each product term is made up of variables or their complements ANDed together. For example, a simple SOP expression might look like:
F = A·B + A’·C
In this expression:
- – A·B is one product term (A AND B)
- – A’·C is another product term (NOT A AND C)
- – The plus sign represents the OR operation
When implementing digital circuits, the sum of products form provides a standardized approach to converting truth tables into logical expressions. This makes it an essential tool in the digital designer’s toolkit.
Minterms: The Building Blocks of SOP
To truly understand SOP, we need to talk about minterms. A minterm is a product term where each variable appears exactly once, either in its normal or complemented form. For a function with n variables, there are 2^n possible minterms. Each minterm corresponds to exactly one row in a truth table where the output is 1. For example, with three variables (A, B, C), the minterm m₃ (which is binary 011) would be written as A’·B·C. This minterm is true only when A=0, B=1, and C=1. Understanding how to derive the sum of products from a truth table is essential for digital electronics students. Let’s look at how to do this with a simple example.
How to Calculate Sum of Products from a Truth Table
Learning how to calculate sum of products expressions starts
with identifying the minterms from a truth table. Let’s walk through this
process step by step:
Create: a truth table for your Boolean function
Identify: all rows where the output is 1
Write: the minterm for each of these rows
Combine: all minterms with OR operations
Let’s try an example with a three-variable function: Looking at this table, we see that F=1 when:
- – A=0, B=0, C=1 (minterm m₁)
- – A=0, B=1, C=1 (minterm m₃)
- – A=1, B=0, C=0 (minterm m₄)
- – A=1, B=1, C=0 (minterm m₆)
So our SOP expression would be:
F = A’·B’·C +A’·B·C + A·B’·C’ + A·B·C’
Or using sigma notation:
F =Σm(1,3,4,6)
This sum of products tutorial example demonstrates the
direct relationship between truth tables and SOP expressions. Once you’ve
practiced this a few times, it becomes second nature.
Canonical and Non-Canonical Forms of SOP
When working with sum of products expressions, you’ll
encounter two main forms: canonical and non-canonical.
Canonical SOP Form
A canonical SOP expression (also called the “standard” form)
includes all variables in each product term. This means that for a function
with n variables, each product term contains exactly n literals. The canonical
form directly corresponds to the minterms from a truth table. It’s complete and
unambiguous, but often not the most efficient representation. For example, the
canonical SOP form of a function might be:
F = A’·B’·C +A’·B·C + A·B’·C’ + A·B·C’
Non-Canonical SOP Form
A non-canonical SOP expression is any SOP expression where
at least one product term doesn’t include all variables. These forms are
typically the result of simplification. For example, the above canonical
expression might simplify to:
F = B’·C’ + A’·C +A·B
This non-canonical form is more compact and would require
fewer gates to implement, making it preferable for practical circuit design. Understanding
these canonical forms is crucial for digital logic design, as they provide a
standardized starting point for circuit optimization.
Difference Between Sum of Products and Product of Sums
The fundamental difference between sum of products and product of sums lies
in their logical structure and implementation.
Sum of Products (SOP)
ü Structure: OR of AND terms
ü Based on: Minterms (combinations that make the function true)
ü Circuit implementation: AND gates feeding into OR gates
ü Truth table derivation: Focus on rows where output is 1
Product of Sums (POS)
· Structure: AND of OR terms
· Based on: Maxterms (combinations that make the function false)
· Circuit implementation: OR gates feeding into AND gates
· Truth table derivation: Focus on rows where output is 0
Understanding the difference between sum of products and
product of sums helps in choosing the most efficient implementation for a
specific circuit. Sometimes one form leads to a simpler circuit than the other.
For example, the function we derived earlier as F = A’·B’·C + A’·B·C + A·B’·C’ + A·B·C’
Could be expressed in POS form as:
F =(A+B+C)·(A+B+C’)·(A+B’+C)·(A’+B+C)·(A’+B’+C’)
Depending on the specific function and available components,
one form might be more practical than the other.
Simplifying Boolean Expressions Using Sum of Products
Once you have a canonical SOP expression, the next step is often
simplification. Simplifying Boolean expressions using sum of products can
significantly reduce the number of gates needed in your circuit. There are
several methods for simplification:
1. Boolean Algebra Laws
Boolean algebra provides the mathematical foundation for
working with sum of products expressions in digital logic. By applying laws
such as:
o Idempotent Law: A + A = A and A · A = A
o Complementary Law: A + A’ = 1 and A · A’ = 0
o Absorption Law: A + (A · B) = A and A · (A + B) = A
You can often simplify expressions by hand. For example: F = A’·B’·C + A’·B·C Can be simplified to:F = A’·C·(B’ + B)= A’·C·1 = A’·C
2. Karnaugh Maps
A Karnaugh map offers a visual method for simplifying sum of products
expressions by identifying adjacent minterms. This technique is especially
powerful for functions with up to 5-6 variables. Digital designers often use
the Karnaugh map technique to find the minimal sum of products form of a
Boolean function. The process involves:
Creating: a grid where each cell represents a minterm
Marking: cells where the function is true
Grouping : adjacent marked cells in powers of 2 (1, 2, 4, 8, etc.)
Deriving : simplified terms from each group
The process of grouping cells in a Karnaugh map directly corresponds to finding common terms in a sum of products expression. This
visual approach often makes it easier to spot simplification opportunities that might be missed with algebraic methods.
3. Quine-McCluskey Algorithm
For functions with many variables, algorithmic approaches like Quine-McCluskey provide a systematic way to find the minimal SOP form. While
beyond the scope of this article, this method is important for complex digital systems where manual simplification becomes impractical.
Applications of Sum of Products in Digital Logic Design
In digital logic design, the sum of products approach is commonly used for implementing combinational circuits. Let’s explore some real-world applications:
1. Combinational Logic Circuits: SOP expressions are
directly implementable as two-level AND-OR circuits, making them ideal for:
a. Decoders and encoders
b. Multiplexers and demultiplexers
c. Arithmetic circuits (adders, subtractors)
d. Comparators
For example, a 4-bit magnitude comparator can be implemented
using SOP expressions to determine whether one number is greater than, equal
to, or less than another.
2. Programmable Logic Devices
Modern programmable logic devices like FPGAs (Field-Programmable Gate
Arrays) and CPLDs (Complex Programmable Logic Devices) often use
sum-of-products structures internally. Their architecture is well-suited to
implementing Boolean functions in SOP form.
3. Memory Address Decoding
In computer systems, address decoders use SOP logic to
activate the correct memory chip based on the address lines. This is a perfect
application for SOP because each memory chip needs to be activated for specific
address combinations.
4. Error Detection and Correction
Digital communication systems use SOP-based circuits for error detection
and correction. Parity generators and checkers, for instance, can be
efficiently implemented using sum of products expressions. These examples of
sum of products in digital logic demonstrate the versatility and importance of
this concept in modern digital systems.
Tools and Software for SOP Implementation
several tools can help you work with sum of products expressions:
1. Logic Circuit Simulators
Logisim : An educational tool for designing and
simulating digital logic circuits. It allows you to create circuits using AND,
OR, and NOT gates to implement SOP expressions.
CircuitVerse : An online platform for digital logic design with a
user-friendly interface.
Digital Works: A comprehensive digital logic simulator that
supports hierarchical designs.
2. Hardware Description Languages (HDLs)
Verilog and VHDL: Industry-standard HDLs that allow you to
describe digital circuits at various levels of abstraction. You can directly
implement SOP expressions in these languages.
SystemVerilog: An extension of Verilog with additional features for
verification and modeling.
3. Boolean Expression Calculators
Wolfram Alpha: Can simplify Boolean expressions and convert between
different forms.
Boolean Algebra Calculator: Online tools specifically designed for Boolean
algebra operations.
K-Map Minimizer: Web applications that generate Karnaugh maps and find minimal
SOP expressions. These tools make working with SOP expressions more efficient
and less error-prone, especially for complex functions.
Future Trends in Digital Logic Design
The field of digital logic design continues to evolve, with several trends
shaping its future:
1. Integration with AI and Machine Learning
As artificial intelligence becomes more prevalent, there’s increasing
interest in optimizing digital logic for AI applications. This includes
specialized circuits for neural network operations, which often rely on
efficient Boolean function implementations.
According to recent industry reports, 77% of executives recognize
the need for rapid AI adoption in their digital infrastructure, though only 25%
believe they have adequate systems in place.
2. Quantum Computing Interfaces
Quantum computing requires interfaces with classical digital logic. This
creates new challenges and opportunities for Boolean function implementation,
including specialized SOP forms that can efficiently communicate with quantum
systems.
3. Low-Power Design
With the growing importance of mobile and IoT devices, power efficiency has
become critical. This has led to renewed interest in logic minimization
techniques, as simpler circuits generally consume less power.
4. Advanced Synthesis Tools
Modern logic synthesis tools are becoming increasingly sophisticated,
automatically finding optimal implementations for Boolean functions. These
tools often use advanced algorithms that go beyond traditional SOP
minimization. These trends suggest that while the fundamental concepts of sum
of products will remain important, their application will continue to evolve
with technological advances.
Conclusion: Mastering the Foundation of Digital Logic
The sum of products is more than just a theoretical concept it’s
a practical tool that forms the foundation of digital circuit design. From
simple logic gates to complex computer systems, SOP expressions provide a
standardized way to implement Boolean functions in hardware.
By understanding how to derive, simplify, and implement sum
of products expressions, you gain insight into how digital systems work at
their most fundamental level. This knowledge is valuable whether you’re
designing circuits, studying computer architecture, or simply curious about the
technology that powers our modern world.
As we’ve seen, there are various tools and techniques
available to help you work with SOP expressions, from Boolean algebra and
Karnaugh maps to specialized software and hardware description languages. Each
approach has its strengths, and mastering them gives you flexibility in
tackling different types of problems.
Whether you’re just starting your journey in digital logic
or looking to deepen your understanding, I hope this guide has provided
valuable insights into the world of sum of products expressions. What aspect of
digital logic design are you most interested in exploring next? Let me know in
the comments below!
