Why This Guide Matters: Understanding Logic Gates
Logic gates are the fundamental building blocks of digital electronics, acting as the “decision-makers” behind every microprocessor. While most textbooks focus on abstract theory, this guide bridges the gap between Truth Tables and Practical Circuit Design. By processing binary signals (0 and 1) through Boolean algebra, these components enable everything from simple calculators to AI-driven hardware. Whether you need to simplify a circuit using De Morgan’s Theorem or leverage Universal Gates (NAND/NOR) for efficient manufacturing, you’ll find the practical answers right here.
Table of Contents
Decoding Digital Brains: How Logic Gates Work
Ever wondered how a computer actually “thinks”? It doesn’t use words; it uses a puzzle of logic gates. After hours of tinkering with circuit diagrams, I’ve realized that these tiny components are the alphabet of the digital world. Whether you’re a hobbyist building your first circuit or a student prepping for exams, this guide simplifies everything from truth tables to Boolean logic with practical, real-world examples.
💡 Pro-Tip: De Morgan’s Theorem
1. NOT (A AND B) = (NOT A) OR (NOT B)
2. NOT (A OR B) = (NOT A) AND (NOT B)
This theorem is the key to simplifying complex circuits and reducing transistor counts in modern CPUs.
Introduction to Basic Logic Gates with Truth Tables
What Are Logic Gates?
| Gate Type | Simple Rule (In Urdu/Hindi) | Best Use Case |
|---|---|---|
| AND Gate | Dono switches ON honge tabhi output aayega. | Safety interlocks (e.g., Lift doors) |
| OR Gate | Koi bhi ek switch ON ho jaye toh kaam chal jayega. | Burglar Alarms |
| NAND Gate | “Universal Hero” – Sab kuch bana sakta hai. | Memory Chips (NAND Flash) |
From Binary Basics to Quantum Logic
Logic gates are the fundamental alphabet of every computer system, translating binary signals (1 and 0) into complex decisions via Boolean algebra. While traditional computing relies on billions of CMOS or MOSFET transistors switching at incredible speeds, the technology is evolving. Today, advanced cryogenic CMOS is integrating with quantum chips to achieve near-perfect fidelity (99.99%), bridging the gap between classical and fault-tolerant quantum computing. Whether you are working with the “Big Seven” (AND, OR, NOT, NAND, NOR, XOR, XNOR) on a breadboard or designing AI-driven hardware, mastering these gates means understanding the very core of how machines “think” and process the digital world.
Understanding Binary Logic and Boolean Algebra

Before we jump into the gates themselves, let’s look at the math behind them. Boolean algebra, named after George Boole, is a simple form of algebra where every value is either true (1) or false (0). It’s perfect for digital circuits because it matches their on-off behavior. In Boolean algebra, a 1 stands for a true state or high voltage, and a 0 stands for false or low voltage. The operations are straightforward: AND acts like multiplication, OR like addition, and NOT flips the value, like a negative sign. When I first learned this, I thought of it as algebra stripped down to just two numbers, which makes digital systems so reliable there’s no gray area, just clear 1s and 0s.
(Pro tip: Ternary NAND gates use modified Fredkin reversible gates for error-free operations in DSP hardware.)
2025 Expert Insight: In quantum digital design, Boolean algebra extends to ternary logic gates (0, 1/2, 1) via Huawei’s patented CMOS-based ternary circuits, reducing gate count by 30% and power by 20% for AI neural networks a shift from binary for ultra-efficient edge computing.
This Boolean logic lets us describe what logic gates do mathematically. For example, voltage signals in circuits are measured relative to ground, where no voltage is a 0 and full voltage is a 1. Logic gates are like specialized amplifiers designed to handle these binary signals, turning inputs into predictable outputs based on their rules. Understanding this foundation makes the gates themselves much easier to grasp.
The Seven Logic Gates with Symbols and Truth Tables
There are seven basic logic gates that power all digital systems. Each has a unique job, a specific symbol, a mathematical rule called a Boolean expression, and a truth table showing how inputs produce outputs. Most gates take two or more inputs, except for one, and their truth tables list every possible input combination. Let’s go through each gate, with its symbol, rule, truth table, and a real-world analogy to make it relatable. I’ll also include the mathematical expressions and explain how they work.
AND Gate
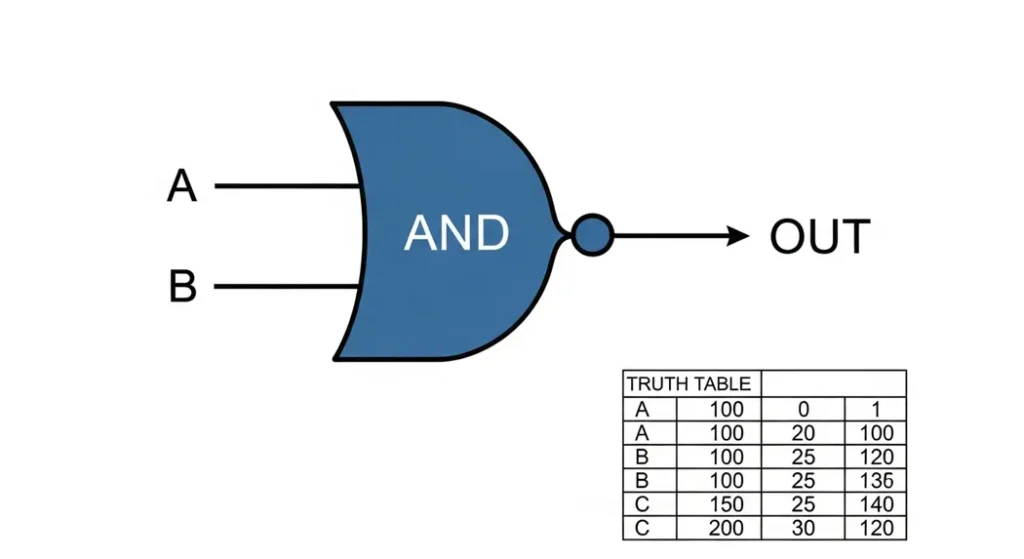
The AND gate is like a strict judge it only says yes, or outputs a 1, when every single input is a 1. If even one input is a 0, the output is 0. Picture it as a series circuit with two switches: the light only turns on if both switches are flipped on. The symbol for an AND gate is a D-shaped figure, flat on the left where inputs enter and curved on the right where the output comes out. Mathematically, it’s written as A · B, or sometimes just AB, meaning both A and B must be true for the output to be true.
The truth table for a two-input AND gate shows this clearly: when inputs A and B are both 0, the output is 0; when A is 0 and B is 1, or vice versa, the output is still 0; only when both are 1 does the output become 1. This gate is used in systems where multiple conditions must be met, like a security system that needs both a keycard and a PIN to unlock a door.
Truth Table for 2-Input AND Gate:
| Input A | Input B | Output |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
OR Gate
The OR gate is more forgiving it says yes, or outputs a 1, if at least one input is a 1. It only outputs a 0 if all inputs are 0. Think of it as a parallel circuit: if either switch is on, the light glows. Its symbol looks like a shield, curved on the left for inputs and pointed on the right for output. The Boolean expression is A + B, meaning the output is true if A or B or both are true.
The truth table for a two-input OR gate shows that the output is 0 only when both A and B are 0; otherwise, it’s 1. This gate is handy in systems where any one condition can trigger an action, like a car’s warning light that activates if either the door is open or the seatbelt is unbuckled.
Truth Table for 2-Input OR Gate:
| Input A | Input B | Output |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
NOT Gate
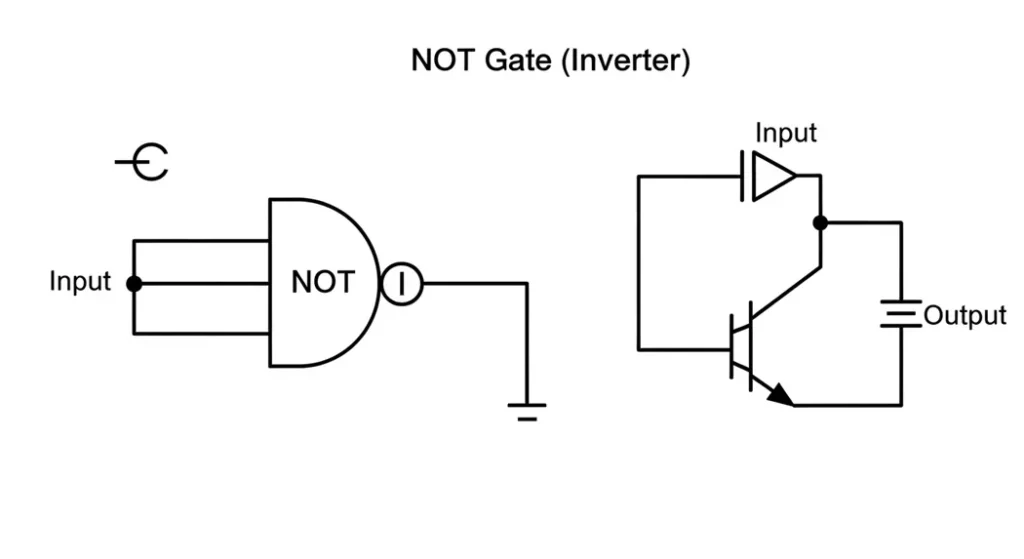
The NOT gate is the rebel it takes one input and flips it. If you give it a 1, it outputs a 0; give it a 0, it outputs a 1. It’s like a light switch that’s normally on but turns off when you press it. The symbol is a triangle with a small circle, called a bubble, at the output to show inversion. Mathematically, it’s written as Ā or A’, meaning “not A.”
The truth table is simple: input 0 gives output 1, and input 1 gives output 0. This gate is crucial for building other gates like NAND and NOR and is used in circuits to reverse signals, like turning off an LED when a button is pressed.
Truth Table for NOT Gate:
| Input | Output |
| 0 | 1 |
| 1 | 0 |
NAND Gate
The NAND gate, short for NOT-AND, combines an AND gate with a NOT gate. It outputs the opposite of an AND gate: it gives a 0 only when all inputs are 1, and a 1 otherwise. Imagine a system where a machine stops only if all sensors detect a problem. The symbol is an AND gate with a bubble at the output. The Boolean expression is (A · B)’, meaning the AND result is inverted.
The truth table shows that with inputs 00, 01, or 10, the output is 1; only with 11 is it 0. I once built an alarm system using NAND gates alone, amazed at how versatile they are. This gate is used in circuits where you need a signal unless all conditions are met, like a safety override.
Truth Table for 2-Input NAND Gate:
| Input A | Input B | Output |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
NOR Gate
The NOR gate, or NOT-OR, is an OR gate followed by a NOT gate. It outputs a 1 only when all inputs are 0; any 1 input gives a 0 output. Think of a system that activates only if no conditions are met, like a standby mode. The symbol is an OR gate with a bubble at the output. The Boolean expression is (A + B)’, meaning the OR result is inverted.
The truth table shows a 1 output only for inputs 00; inputs 01, 10, or 11 give 0. NOR gates are used in circuits like memory latches, where you need a signal only when nothing is active.
Truth Table for 2-Input NOR Gate:
| Input A | Input B | Output |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
XOR Gate
The XOR gate, or Exclusive OR, outputs a 1 when an odd number of inputs are 1. For two inputs, it’s 1 when they’re different, 0 when they’re the same. It’s like a hallway light with two switches: flipping either one changes the light’s state, but flipping both cancels out. The symbol is an OR gate with an extra curved line on the input side. The Boolean expression is A ⊕ B, or A’B + AB’, meaning one input is true but not both.
The truth table shows 0 for inputs 00 and 11, and 1 for 01 and 10. XOR gates are used for addition in arithmetic circuits and error detection in communications.
Truth Table for 2-Input XOR Gate:
| Input A | Input B | Output |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
XNOR Gate
The XNOR gate, or Exclusive NOR, outputs a 1 when an even number of inputs are 1. For two inputs, it’s 1 when they’re the same, 0 when different. It’s like XOR followed by NOT. The symbol is an XOR with a bubble at output. The expression is A ⊙ B or A’B’ + AB.
The truth table shows 1 for 00 and 11, 0 for 01 and 10. XNOR is used for equality checks and in adders.
Truth Table for 2-Input XNOR Gate:
| Input A | Input B | Output |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Universal Gates: NAND and NOR
Why NAND and NOR are Universal Gates
NAND and NOR gates are special because they are universal you can build any logical function using just one type. This makes them incredibly valuable in circuit design because they are simple and cheap to manufacture in integrated circuits. Whether you are working on AI hardware or custom FPGA designs, these gates allow for scalable networks with fewer transistors.
Practical Implementation: NAND Gate Conversions
NAND gates can mimic the three core operations: AND, OR, and NOT. Here is how the logic works:
- 1. NOT Gate: Connect both inputs of a NAND gate together.
If input is A, output is (A · A)' = A', or NOT A. - 2. AND Gate: Take a NAND gate and follow it with a NAND-based NOT gate.
This reverses the inversion, giving A · B. - 3. OR Gate: Invert each input using NAND-based NOT gates, then feed them into another NAND.
Formula: (A' · B')' = A + B.
Note on NOR Gates: Using NOR gates works in a similar cascading setup. A NOT gate is a NOR with both inputs tied: (A + A)' = A'. An OR gate is a NOR followed by a NOR-based NOT gate, while an AND gate is made by inverting inputs before feeding them into a NOR gate: (A' + B')' = A · B.
Engineer’s Secret: Why NAND and NOR Rule the Industry
Ever wondered why manufacturers don’t use 7 different types of gates on a chip? It’s all about economies of scale. By using only NAND or NOR gates, companies can mass-produce a single transistor architecture, reducing manufacturing costs and circuit size. This is why mastering “Universal Gate Conversion” is a critical skill for any hardware engineer.
Digital Logic Performance: Key Metrics and Formulas
In high-speed circuit design, a gate is defined not just by its truth table, but by its speed and power consumption. Engineers use the following formulas and metrics to select the correct Integrated Circuit (IC) family (e.g., 74HC vs. 74LVC):
1. Propagation Delay (t_pd)
Propagation delay is the time required for a signal to travel from the input of a gate to the output. It is the primary measure of a gate’s speed. Designers must consider both the Low-to-High ( t p L H ) and High-to-Low ( t p H L ) transitions .
t pd = t p L H + t p H L 2
Typical CMOS logic gates have a propagation delay measured in **nanoseconds (ns)**. Minimizing this delay is crucial for microprocessor clock speeds.
2. Power-Delay Product (PDP)
The Power-Delay Product is the gold standard for efficiency, representing the amount of energy consumed per switching operation. It balances speed and power consumption.
PDP = P avg × t pd
Where $P_{\text{avg}}$ is the average dynamic power consumed by the gate. Modern logic families are optimized to achieve a lower PDP, saving battery life in portable devices.
Uses of Logic Gates in the Real World
Logic gates are everywhere, powering the devices we use daily. Their behavior, defined by truth tables, determines how they’re applied. In computers, they form the backbone of CPUs, which contain billions of gates. For example, arithmetic operations like addition rely on circuits called adders, made from XOR and AND gates. Memory storage uses flip-flops, built from NAND or NOR gates, to store bits. Every click or keystroke on your laptop goes through logic gates to process the input.
(Beginner tip: This means future computers won’t crash from errors; experts can implement it in Qiskit for hybrid quantum-classical circuits.)
2025 Pro Insight: In quantum hardware, logic gates evolve to ‘error-transparent gates’ using parity-nested operations on binomial-encoded qubits (NIST/Oxford breakthrough), enabling distributed quantum algorithms across networked processors – a game-changer for fault-tolerant AI hardware with 99.9975% fidelity (Quantinuum Helios).**
In consumer electronics, gates are just as critical. Your TV remote uses them to encode button presses into signals. Digital cameras process image data with logic circuits. Gaming consoles rely on gates for everything from reading controller inputs to rendering graphics on the screen. I built a simple LED display circuit once, and seeing the gates control each light was a thrill.
Security systems make clever use of gates. An alarm might use an AND gate to trigger only when multiple sensors like a door and motion detector are active. Password systems use XOR gates to compare your input to a stored code, ensuring they match. Keypad locks combine gates to check if the right button sequence is pressed, like in a bank vault.
In cars, logic gates are vital. Anti-lock braking systems process sensor data with gates to prevent wheel lockup. Engine control units use complex gate arrays to optimize fuel and timing. Dashboard lights, like low-fuel warnings, activate based on gate logic when conditions are met, such as low fuel and engine on.
Beyond these, gates are used in smart home devices, like an IoT system that turns on lights only when it’s dark and motion is detected, using an AND gate. In AI hardware, gates form neural network circuits for fast computations. There’s no limit to how many gates you can combine, though physical space in a chip sets practical boundaries. As chip technology improves, we pack more gates into smaller spaces, making devices faster and more powerful.
Advanced Logic Gate Diagnostics and Troubleshooting
Beyond simple continuity checks, professional digital troubleshooting requires analyzing timing and noise characteristics using an oscilloscope.
Using Timing Diagrams for Fault Isolation
Timing diagrams are essential tools for verifying that sequential logic circuits (like flip-flops and counters) are operating correctly. An oscilloscope is used to visualize signal transitions in real-time. Faults such as glitches or metastability appear as timing violations:
- Glitches: Unintended, very short pulses (often due to race conditions) that can be isolated by observing the t p L H and t p H L delays between cascaded gates.
- Clock Skew: A common issue where the clock signal arrives at different gates at slightly different times, which is diagnosed by measuring the rising edge arrival time across multiple clock pins.
Noise Margin and Fan-Out Constraints
Two critical professional metrics define gate reliability in a complex circuit:
- Noise Margin ( N M ): The maximum voltage noise (unwanted signal) a gate can tolerate without altering its output. It is calculated from the voltage thresholds ( V OH , V OL , V IH , V IL ) and is a core measure of gate robustness.
- Fan-Out: The maximum number of standard loads (inputs of other gates) that the output of a single gate can reliably drive while maintaining specified voltage levels and timing constraints. Exceeding the fan-out limit causes signal degradation and increased propagation delay.
How Logic Gates Work Physically
To really get logic gates, you need to know how they work at the hardware level. They’re built from transistors inside integrated circuits, or ICs. There are two main technologies: TTL, or Transistor-Transistor Logic, which uses bipolar transistors for fast switching but consumes more power, typically at 5 volts; and CMOS, or Complementary Metal-Oxide-Semiconductor, which uses field-effect transistors for lower power use and can work at various voltages, like 3.3 or 5 volts. CMOS is more common today because it’s energy-efficient.
(Pro application: Use in QEC for 99.7% fidelity two-qubit gates; beginners can simulate in Logisim.)
2025 Advanced: Cryo-CMOS control chips (SemiQon/VTT EARTO award winner) integrate logic gates at 4K temperatures for quantum processors, reducing readout wiring by 30% and enabling 5,000-gate circuits on IBM Nighthawk – ideal for scalable logical qubits in fault-tolerant systems.
Inside a chip, transistors act like tiny switches, either on or off, matching the 1 and 0 of binary logic. For example, in a CMOS AND gate, when both inputs are high, the transistors create a path to the output, giving a 1. If either input is low, the path breaks, outputting 0. This clear on-off behavior makes digital circuits reliable, unlike analog circuits where signals can vary. In diagrams, we often skip showing power connections to keep things simple, but gates need a voltage supply to work.
Industry Standards: The 7400 Series and Digital IC Compliance
All basic logic gates are manufactured under rigorous standards to ensure compatibility and reliability. The most common standard series is the 7400-series (TTL/CMOS):
Key IC Series and JEDEC Standards
- 74HC (High-speed CMOS): The industry workhorse for low-power digital designs. It offers low static power consumption but higher dynamic power consumption than newer families.
- 74LVC (Low-Voltage CMOS): Used in modern 3.3V and 1.8V systems (like microprocessors) and optimized for low-voltage, high-speed switching to minimize power-delay product (PDP).
- JEDEC Standards: Logic gates must comply with Joint Electron Device Engineering Council (JEDEC) standards, which dictate parameters like pin configurations, operating temperature ranges, and maximum rated voltages.
Electrostatic Discharge (ESD) and Latch-Up Safety
A critical safety and reliability note: CMOS gates are highly susceptible to damage from Electrostatic Discharge (ESD). Professional handling requires grounding straps. Furthermore, an internal circuit failure called **latch-up** can cause the IC to short the power supply to ground, often triggered by transient spikes—a major consideration in robust circuit design.
Advantages and Challenges of Logic Gates
Logic gates are amazing but not perfect. They’re reliable because digital signals resist noise unlike analog signals, which can pick up interference. Their outputs are predictable, making complex systems consistent. You can combine them endlessly to build anything from a calculator to a supercomputer, and they follow standard designs for easy integration. Modern CMOS gates use very little power when idle, which is why your phone battery lasts.
But there are challenges. Gates take a tiny fraction of a second to respond, called propagation delay, which can limit speed in fast circuits. They use more power when switching states, and in dense chips, this generates heat. They’re not great for analog signals without extra conversion. In extreme environments, like space, radiation can flip bits, causing errors. I once worked on a high-speed project where we had to tweak the design to account for delays, a real lesson in planning.
Experimenting with Logic Gates
The best way to learn logic gates is by experimenting. Start with breadboard circuits using 7400‑series ICs: wire switches and LEDs to watch truth tables in action. For virtual practice, use simulators like Logisim or CircuitVerse to test complex designs without hardware. Microcontrollers such as Arduino can mimic gate logic in code, while FPGAs let you program hardware directly—sculpting logic in silicon.
A simple AND gate demo or a half‑adder with XOR and AND shows how binary arithmetic works.
Common questions:
- Digital vs. analog? Digital uses 0/1, analog uses continuous signals.
- Why NAND/NOR are universal? Any logic function can be built from them.
- How do gates fail? Overheating, voltage spikes, or radiation can damage transistors.
- How to troubleshoot? Check power, probe inputs, inspect connections, and replace faulty ICs.
- De Morgan’s Theorem? Simplifies NAND/NOR expressions, vital for modern CPU and AI hardware design.
2025 Update: De Morgan’s theorem now optimizes ternary logic in cryo‑CMOS AI chips, reducing quantum cost and latency in error‑corrected qubits.
Wrapping up:
Logic gates turn simple binary signals into the complex systems behind calculators, CPUs, and AI processors. Mastering their truth tables and rules gives you a clear window into how computers make decisions.
Frequently Asked Questions
1. What are logic gates in simple terms?
Logic gates are the fundamental building blocks of digital circuits. They act as electronic switches that process binary signals (0 and 1) based on Boolean logic to perform computational tasks.
2. How many types of logic gates are there?
There are seven primary logic gates: AND, OR, NOT (Basic Gates), NAND, NOR (Universal Gates), and XOR, XNOR (Arithmetic/Special Gates).
3. Why are NAND and NOR called “Universal Gates”?
They are called universal because any other logic gate (AND, OR, NOT) can be created using only NAND or only NOR gates. This simplifies integrated circuit (IC) manufacturing by using a single type of component.
4. What technology is used to build modern logic gates?
Modern gates are primarily built using CMOS (Complementary Metal-Oxide-Semiconductor) or MOSFET technology. In cutting-edge quantum computing, cryogenic CMOS is used to achieve near-perfect signal fidelity.
5. How does binary math relate to logic gates?
Binary math uses 0 and 1, which corresponds to the ‘OFF’ and ‘ON’ electrical states of transistors. Logic gates apply Boolean algebra to these binary values to execute computer instructions.
6. What is the difference between an OR gate and an XOR gate?
An OR gate gives a HIGH output if at least one input is 1. An XOR (Exclusive OR) gate gives a HIGH output only if the inputs are different (one is 0, the other is 1).
7. Where are logic gates used in real life?
They are everywhere: in your smartphone’s processor, calculator’s ALU, digital watches, automated street lights, and even safety sensors in washing machines.
8. How does De Morgan’s Theorem help in circuit design?
De Morgan’s Theorem allows engineers to simplify complex Boolean expressions. By converting gates from one type to another (e.g., AND to OR logic), it helps reduce the number of transistors needed on a chip.
9. Can logic gates be built without transistors?
Yes, logic gates can be implemented using diodes, mechanical relays, fluidics, or even optical fibers, though transistors are the most efficient for microelectronics.
10. Why is mastering logic gates essential for AI and Robotics?
AI processors and robot controllers rely on low-latency decision-making at the hardware level. Understanding logic gates is crucial for optimizing the “Edge Computing” chips that drive autonomous systems.



Pingback: The Ultimate Comparison: ESP32 vs Raspberry Pi /