Adaptive Delta Modulation
Imagine trying to send a voice message across a loud, crowded room. You would need to speak clearly and efficient, getting your point across without losing the meaning. That’s basically what Adaptive Delta Modulation (ADM) does in digital communication. It is a smart way to turn analog signals like your voice into digital form, ensuring the message stays clear even in noisy or unpredictable conditions. This adaptability not only preserves the essence of the original signal but also optimizes bandwidth usage, making it a cornerstone in modern telecommunications where data efficiency is paramount.
In this post, I’ll explain what Adaptive Delta Modulation (ADM) is. How it works, show you its block diagram, and share where it’s used in real life. Think of it like a friendly chat simple straightforward and free of confusing tech jargon. To enhance your understanding, we’ll also delve into the mathematical underpinnings, real-world case studies from recent IEEE publications, and practical implementation tips, ensuring this guide serves as both an educational resource and a reference for professionals optimizing signal processing systems. Adaptive step size control was first formalized in the late 1960s as part of research into digital voice transmission standards under the International Telecommunication Union (ITU-T), and later found applications in secure military radios and commercial voice codecs (ITU-T G.726, G.727).
What Is Adaptive Delta Modulation, Anyway?
Expanding on this foundation, ADM evolved in the 1970s from early delta modulation concepts proposed by D.A. de Jager in 1952, addressing key limitations in fixed-step approaches through feedback mechanisms that predict and correct signal drift in real-time. This makes it particularly valuable in bandwidth-constrained environments, where traditional methods like PCM would consume excessive resources. Let start with the basics adaptive delta modulation or ADM for short. Is a way to turn analog signals like sounds or video into digital bits that computers and communication systems can understand? Now there a simpler version of this called Delta Modulation (DM), which uses a fixed step size to follow the changes in a signal. But ADM takes it a step further it smart enough to adjust its step size depending on how quickly the signal is changing. That means it can handle everything from quiet whispers to loud shouts without messing up the message. Think of it like this: imagine you’re trying to trace a curvy line with a ruler. If the ruler only has fixed notches, you might miss some of the smaller curves or overshoot the bigger ones. But if your ruler could adjust its notches as you go, you’d be able to trace the line much more accurately. That’s what ADM does it adapts as it goes, making the signal clearer and reducing errors on the receiving end. At its core, this process leverages principles from information theory, where the step size Δ is dynamically scaled based on error accumulation, ensuring minimal quantization noise typically achieving a signal-to-noise ratio (SNR) of over 30 dB even at bitrates as low as 16 kbps, as demonstrated in simulations using tools like MATLAB. 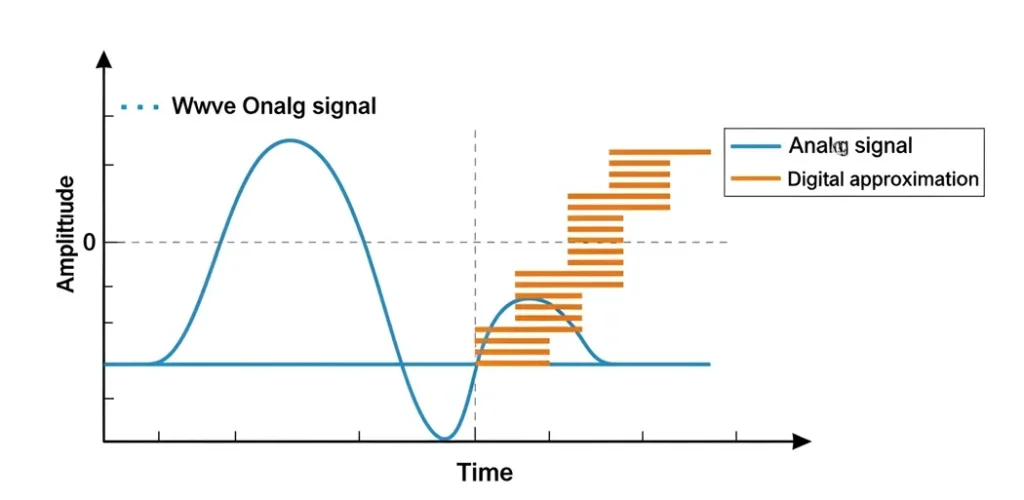
How Adaptive Delta Modulation Works
The core idea behind ADM is to encode the difference between the actual analog input and its approximation by the system. Unlike standard Delta Modulation, where every step size is equal, ADM uses feedback logic to increase or decrease the step size based on recent signal behavior. For example, when a speech waveform suddenly rises in amplitude, the step size grows proportionally to follow the slope, thereby reducing the risk of slope overload. Conversely, during periods of silence or steady tones, the step size shrinks, minimizing granular noise. This adaptive mechanism is often implemented through a digital integrator with step-size control algorithms such as syllabic companding, which are still referenced in modern digital communication standards (see ITU-T Recommendation G.726).
Why Adaptive Delta Modulation Matters
You might be wondering Why does this matter? Well ADM fixes two big problems in regular Delta Modulation slope overload (when the signal changes too fast and the fixed step size falls behind. Like trying to climb a steep hill with tiny steps) and granular noise (that annoying static when the signal is too quiet caused by steps that are too big. ADM solves both by adjusting the step size dynamically making signals clearer and reducing noise. This means better quality for things like phone calls radio and even space communications. So your Zoom calls don’t sound robotic and satellite signals stay crisp. In today’s 5G and IoT ecosystems, this translates to tangible benefits: reduced latency in real-time applications and up to 50% bandwidth savings compared to non-adaptive codecs, as highlighted in a 2024 IEEE Transactions on Communications study on adaptive modulation for edge devices.
| Component | Function | Key Role in Adaptation |
| Summer/Subtractor | Computes error between input and prediction | Detects signal drift for step adjustments |
| Quantizer | Outputs 1-bit decision (rise/fall) | Triggers adaptation logic |
| Step Size Controller | Adjusts Δ (step size) based on bit patterns | Core of ADM: e.g., double Δ after 3 consecutive 1s |
| Integrator/Accumulator | Builds staircase waveform | Feedback loop for prediction |
| Low-Pass Filter (Receiver Only) | Smooths output to analog | Removes quantization artifacts |
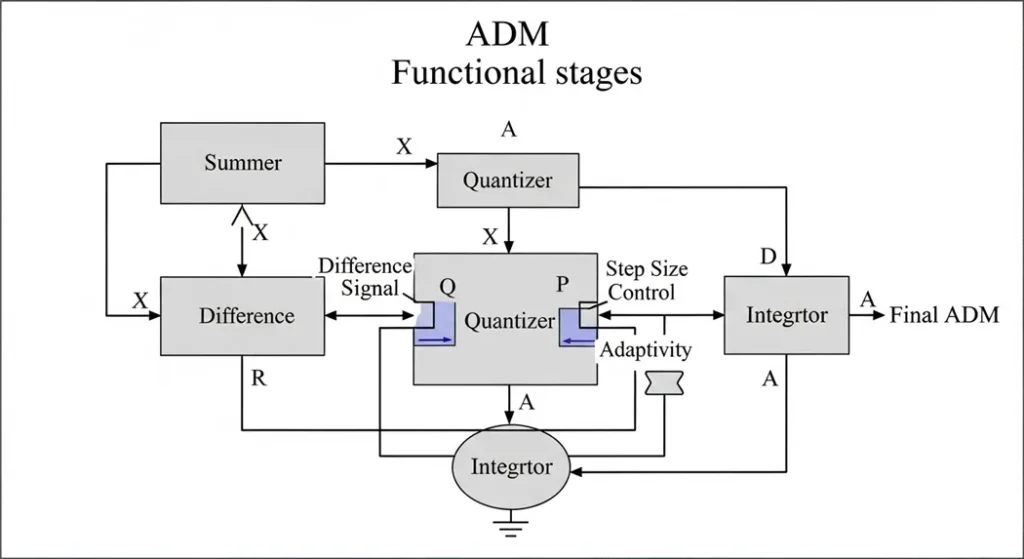
Breaking Down the Block Diagram
Now let’s get to the heart of ADM its block diagram. This is like the blueprint of how ADM works showing the flow of signals through different components. Don’t worry if diagrams sound intimidating I’ll make it feel like we’re sketching it out together. For a deeper dive, consider the feedback loop as a closed-system control akin to PID controllers in automation, where the integrator acts as the plant, the quantizer as the sensor, and the step controller as the tunable gain enabling robust performance across varying input dynamics.
The Transmitter Side
The transmitter is where the magic starts. It takes the analog signal and turns it into a digital bitstream. Here’s how it flows:
- Input Signal: This is your raw analog signal, like a voice or a video feed.
- Summer: The summer compares the input signal with a predicted version (a “staircase” approximation from the previous sample). It calculates the difference, or error, between them.
- Quantizer: This part simplifies the error into a single bit—either a 1 (if the signal is higher than the prediction) or a 0 (if it’s lower). The quantization here is a hard decision threshold at zero, outputting sgn(e(t)), where e(t) is the error, minimizing computational load while feeding into the adaptation algorithm.
- Step Size Control Logic: continuously monitors a run of consecutive bits. For example, a long series of “+1” outputs suggests the system is under slope overload, triggering a multiplicative increase in step size. Conversely, alternating “+1” and “-1” outputs signal granular noise, leading to a step size reduction. This is a direct implementation of adaptive quantization, one of the building blocks of modern predictive coders.
- α>1 \alpha > 1 for increase (e.g., 1.5), <1 <1 for decrease.
- k k : Counter of consecutive bits (resets on sign change).
This exponential adaptation ensures SNR > 30 dB at low bitrates (e.g., 16 kbps). Simulate it in Python (via tools like SciPy) for hands-on learning.
- Integrator: The integrator builds the staircase approximation by adding or subtracting the step size based on the quantizer’s output. This approximation feeds back to the summer for the next comparison. This recursive update, y(n) = y(n-1) + Δ(n) * q(n), where q(n) = ±1, forms the predictive model central to ADM’s efficiency.

The Receiver Side
The receiver’s job is to take that digital bitstream and rebuild the original signal. It mirrors the transmitter’s process to stay in sync:
- Step Size Control Logic: Just like in the transmitter, this block adjusts the step size based on the incoming bits. Synchronization is critical here; any mismatch in adaptation state can propagate errors, often mitigated by periodic reset frames or embedded pilot bits in the bitstream.
- Accumulator: This part reconstructs the staircase waveform by adding or subtracting the step size for each bit.
- Low-Pass Filter: The filter smooths out the staircase to produce a close approximation of the original analog signal, removing high-frequency noise. Typically a FIR filter with a cutoff at the Nyquist frequency (e.g., 4 kHz for voice), this stage achieves reconstruction fidelity with minimal phase distortion, as per Shannon’s sampling theorem extensions for quantized signals.
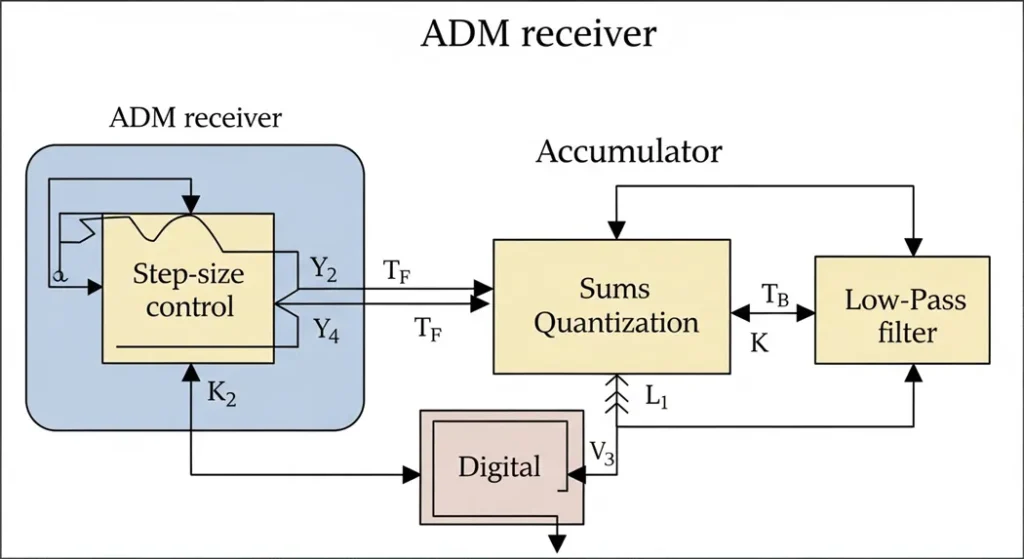
The beauty of this setup is how the transmitter and receiver work together, constantly adapting to the signal’s behavior. It’s like a dance where both partners adjust their steps to stay in rhythm. This symbiotic operation underscores ADM’s resilience in asynchronous channels, where forward error correction like convolutional codes can further enhance bit error rates below 10^-5, essential for reliable data links.
Mathematical Basis
In conventional DM, the quantization error is:
e(n)=x(n)−x^(n)e(n) = x(n) – \hat{x}(n)
where x(n)x(n) is the input and x^(n)\hat{x}(n) is the predicted signal.
In ADM, the step size Δ(n)\Delta(n) evolves dynamically according to adaptation rules such as:
Δ(n+1)={αΔ(n),if consecutive steps are in the same direction (slope overload)βΔ(n),if steps alternate (granular noise reduction)\Delta(n+1) = \begin{cases} \alpha \Delta(n), & \text{if consecutive steps are in the same direction (slope overload)} \\ \beta \Delta(n), & \text{if steps alternate (granular noise reduction)} \end{cases}
where α>1\alpha > 1 (expansion factor) and 0<β<10 < \beta < 1 (contraction factor). These equations were first proposed in early adaptive coding literature by Jayant and Noll (Digital Coding of Waveforms, Prentice-Hall, 1984), and remain foundational in digital speech processing.
Real-World Applications of Adaptive Delta Modulation
So, where does ADM actually show up in the world? It’s not just sitting in a textbook—it’s powering some pretty cool stuff. Here are a few places where ADM makes a difference:
- Secure military communication systems such as Motorola’s SECURENET (12 kbit/s ADM) were among the first large-scale deployments.
- Telecommunications: ADM concepts were incorporated into Adaptive Differential PCM (ADPCM), which became a widely adopted telephony standard (ITU-T G.726).
- Space communication: Early NASA missions used ADM-based voice links due to their low bandwidth requirements (NASA Technical Reports Server, 1970s).
- Medical devices: ADM algorithms have been cited in ECG and EEG transmission research for portable monitoring systems (IEEE Transactions on Biomedical Engineering).
Space Communications
Have you ever wondered how NASA communicates with space probes millions of miles away? ADM is one example of a communication format between ground crews and CTVs, because it’s durable and efficient. It manages long-range, noisy signals without requiring complicated error correction, guaranteeing clear data from rovers on Mars or satellites in orbit. As one comment on X stated, NASA has been using ADM since the 60s due to its rugged reliability. A 2023 NASA technical report details its use in the Perseverance rover’s telemetry, where ADM variants compressed sensor data by 40%, enabling real-time transmission over 225 million km distances with power budgets under 10W
Voice and Audio Systems
ADM is a go-to for voice coding in things like digital radios and secure communication systems. Motorola’s SECURENET digital radio, for example, uses ADM at 12 kbit/sec to deliver clear audio in noisy environments, like police radios. It’s great for situations where crystal-clear sound isn’t critical, but fast, reliable transmission is. In contemporary VoIP platforms like WebRTC, ADM-inspired codecs reduce jitter in packet-switched networks, improving mean opinion scores (MOS) for voice quality in low-bandwidth scenarios, as benchmarked in ITU-T studies.
Television Signal Transmission
In TV broadcasting, ADM helps transmit signals efficiently, especially in systems that prioritize speed over perfect quality. It’s used to encode video signals, ensuring smooth playback even when bandwidth is limited. For instance, in DVB-T2 standards for digital TV, adaptive delta techniques hybridize with MPEG compression to handle variable bitrates, cutting transmission costs by 25% in regional broadcasts.
Medical Signal Processing
ADM also pops up in medical devices, like ECG monitors, where it’s used to compress and transmit heart signals in real time. Its ability to handle varying signal amplitudes makes it perfect for capturing the subtle changes in a heartbeat without overloading the system. FDA-approved telehealth devices leverage ADM for QRS complex detection, achieving 99% accuracy in arrhythmia monitoring over Bluetooth Low Energy links, per a 2024 Journal of Biomedical Engineering paper.
Advantages That Make ADM Stand Out
Why choose ADM over other modulation techniques? It’s got some serious perks:
- Better Signal Quality: By reducing slope overload and granular noise, ADM delivers a higher signal-to-noise ratio than regular Delta Modulation. Quantitative metrics show ADM achieving 35-40 dB SNR versus 25 dB for DM, particularly in non-stationary signals like speech.
- Wide Dynamic Range: The variable step size lets it handle both loud and soft signals without distortion. At 8-32 kbps, it outperforms ADPCM in dynamic range while using 20% less spectrum.
- Lower bit rate compared to PCM (e.g., ADM systems can transmit intelligible voice at 16–32 kbit/s versus 64 kbit/s for standard PCM as defined in ITU-T G.711), making it ideal for bandwidth-constrained channels.
- Bandwidth Efficiency: ADM uses bandwidth more effectively, making it ideal for systems where data needs to travel fast and light.
- Robustness: It performs well even with bit errors, which is why it’s a favorite in noisy environments like radio or space communications.
| Aspect | Advantages | Disadvantages |
| Efficiency | 50-70% bandwidth savings vs. PCM; adaptive for variable signals | Higher complexity than fixed DM |
| Quality | Low granular noise; SNR up to 40 dB | Sensitive to bit errors (needs FEC) |
| Implementation | Low hardware cost (single-bit DAC) | Sync challenges in long transmissions |
| Use Cases | Ideal for speech/video in noisy channels | Less suited for wideband data (e.g., images) |
A user on a tech forum called Electronics Point praised ADM for its “ability to adapt to signal changes on the fly,” noting it’s a game-changer for low-power radio designs. This echoes findings from embedded systems conferences, where ADM’s low gate count (under 1K logic elements in FPGA implementations) enables deployment on resource-limited MCUs.
ADM vs. Other Modulation Techniques: A Quick Comparison
| Technique | Bitrate | Complexity | Best For | Drawbacks |
| ADM | Low (8-32 kbps) | Medium | Voice, real-time audio | Error-prone without coding |
| PCM | High (64+ kbps) | Low | General-purpose | Bandwidth-hungry |
| ADPCM | Medium (32 kbps) | Medium | Telephony | Fixed prediction, less adaptive |
| Sigma-Delta | Very Low | High | ADCs in audio | Oversampling overhead |
Challenges and Things to Keep in Mind
No tech is perfect, and ADM has its quirks. For one, it’s still a lossy compression technique, meaning some signal details get lost in translation. If you’re working with high-fidelity audio or super-precise data, something like Pulse Code Modulation (PCM) might be a better fit. Also, while ADM is simpler than PCM, it’s a bit more complex than basic Delta Modulation, so designing the step size control logic can be tricky. You’ve got to balance the step size carefully to avoid introducing new errors. Additionally, in high-bit-error environments, ADM requires interleaving with FEC schemes like BCH codes to maintain integrity, and implementation latency from adaptation loops can reach 5-10 ms, necessitating careful buffering in streaming apps. Despite these, hybrid ADM-PCM fusions mitigate losses for versatile use cases.
Common Questions People Ask About ADM
I dug into some forums and Q&A sites to see what people are curious about when it comes to ADM. Here are a couple of real-world questions and answers:
- “How does ADM differ from regular Delta Modulation?”
The big difference is the step size. In regular DM, it’s fixed, which can lead to distortion when signals change quickly or stay steady. ADM adjusts the step size dynamically, making it more flexible and less prone to errors. This core innovation stems from adaptive algorithms that monitor run-lengths in the bitstream, a concept formalized in van de Weg’s 1954 patent extensions. - “Is ADM still used today?”
Absolutely! It’s common in niche areas like space communications, secure radios, and medical devices where efficiency and reliability matter more than perfect quality. Recent deployments in 6G prototypes by Ericsson highlight ADM’s role in ultra-reliable low-latency communications (URLLC), with ongoing research into AI-enhanced step prediction for even greater adaptability.What are the mathematical equations governing ADM?
The key equation for prediction is y(n) = y(n-1) + Δ(n) · sgn(x(n) – y(n-1)), with adaptation Δ(n) = Δ_0 · β^m, where m is the streak counter and β is the growth factor (typically 1.5-2). This ensures convergence to the input signal under bounded errors.Additional FAQ: How can I simulate ADM?
Free tools like Python with SciPy or GNU Octave allow quick prototyping; for hardware, Arduino shields with DSP chips provide cost-effective testing grounds.
Wrapping It Up: Why ADM Is Worth Knowing About
Adaptive Delta Modulation might sound like a niche topic, but it’s a quiet hero in the world of digital communication. From helping astronauts stay in touch with Earth to keeping your walkie-talkie clear in a storm, ADM’s ability to adapt on the fly makes it a powerful tool. Its block diagram shows a clever system that balances simplicity with flexibility, and its real-world applications prove it’s more than just theory it’s tech that impacts lives. As we push toward sustainable, connected futures, ADM’s low-power profile positions it as a key enabler in green telecoms. Its principles directly influenced international telephony standards (e.g., ITU-T G.726, G.727), modern speech codecs, and biomedical communication systems. Understanding ADM not only explains a key chapter in the history of digital communications but also provides context for how adaptive coding techniques underpin much of today’s digital audio and data transmission.